本篇讲述 Redis 中的基础数据结构 ZSet(SortedSet) 的底层实现原理和如何通过 go 语言实现一个 ZSet 的过程以及需要注意的问题。
本文章为该系列的
有序集合,如果需要阅读其他相关文章, 请点击
这里 跳转查看
1 前言 使用 Redis 过程中集合这个概念出现的比较频繁,常用的 set,zset 都是集合的概念。与普通的集合不同的是,zset 的元素之间是有顺序的,而且这个顺序不是插入的顺序而是使用者插入元素时指定的 score 而定的。
zset 中的任何元素都是有score 值(浮点数)的,而且根据 score 的顺序进行读写甚至可以做到获取范围数据,这些特性给使用者带来了无数种可能性解决方案。
从使用者的角度来说,zset 更像一个 kv 结构,元素不可以重复但是不同元素的 score 值是可以一样的,此时的排序是按元素字典排序。
通过 ZRANGEBYSCORE 命令可以列出指定score范围内的元素以及对应的 key,
其顺序为 score 的升序。
1
2
3
4
5
6
7
> ZRANGEBYSCORE zset1 0 100 withscores
1) "a"
2) "5"
3) "b"
4) "5"
5) "hello"
6) "20"
2 zset 支持的能力 zset 作为一个有序集合,即拥有普通集合的特性,同时又基于其有序特性衍生出更多别的特性。主要特性如下:
元素不重复 集合之间交集并集差集的操作 批量读写元素 根据 score 操作(增删改查)元素 获取score最大最小的元素 根据集合内rank(或 index)操作(增删改查)元素 3 zset 底层原理
本篇中所有引用的 Redis 源码均基于 Redis6.2 版本。
Redis 实现的 zset 底层是跳跃表和哈希表的组合。跳跃表 用于记录和操作所有基于 score 的操作,而哈希表存的是元素值和 score 的kv关系,用于快速定位元素存不存在的情况。
1
2
3
4
typedef struct zset {
dict * dict ; // 哈希表,存储 元素->score
zskiplist * zsl ; // 跳跃表
} zset ;
除了跳跃表和哈希表之外,其实还有一个不怎么出场的数据结构 – ziplist(压缩列表)。在满足以下两个条件的情况下,Redis 会使用 ziplist来替代跳跃表。
保存的元素少于128个 保存的所有元素大小都小于64字节 在了解跳跃表之前先了简单解一下 ziplist 这个数据结构的实现以及解答为什么要用 ziplist 来替代跳跃表。
3.1 压缩列表-ziplist ziplist 编码的有序集合对象使用压缩列表作为底层实现,每个集合元素使用两个紧挨在一起的压缩列表节点来保存,第一个节点保存元素的成员,第二个节点保存元素的分值。并且压缩列表内的集合元素按分值从小到大的顺序进行排列。
从上述的两个条件可以看出,在数据量少且单个元素也比较小的情况下,使用 ziplist 是为了节省内存,因为在数据量少的情况下发挥不出来 skiplist 的优势且占的内存比 ziplist 大。
想更深入了解 ziplist 的实现细节,请点击 这里查看
1
2
3
4
5
6
7
8
9
10
11
area |< ---- ziplist header ---- > |< ----------- entries ------------- > |< -end- > |
size 4 bytes 4 bytes 2 bytes ? ? ? ? 1 byte
+---------+--------+-------+--------+--------+--------+--------+-------+
component | zlbytes | zltail | zllen | entry1 | entry2 | ... | entryN | zlend |
+---------+--------+-------+--------+--------+--------+--------+-------+
^ ^ ^
address | | |
ZIPLIST_ENTRY_HEAD | ZIPLIST_ENTRY_END
|
ZIPLIST_ENTRY_TAIL
1
2
3
4
5
area |< ------------------- entry -------------------- > |
+------------------+----------+--------+---------+
component | pre_entry_length | encoding | length | content |
+------------------+----------+--------+---------+
3.2 跳跃表-skiplist 3.2.1 定义 跳跃表是一个随机化的数据结构,实质就是一种可以进行二分查找的有序链表。跳跃表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。跳跃表不仅能提高搜索性能,同时也可以提高插入和删除操作的性能。
它采用随机技术决定链表中哪些节点应增加向前指针以及在该节点中应增加多少个指针。跳跃表结构的头节点需有足够的指针域,以满足可能构造最大级数的需要,而尾节点不需要指针域。
采用这种随机技术,跳跃表中的搜索、插入、删除操作的时间均为O(logn),然而,最坏情况下时间复杂性却变成O(n)。相比之下,在一个有序数组或链表中进行插入/删除操作的时间为O(n),最坏情况下为O(n)。
3.2.2 原理 跳跃表原理非常简单,在链表的基础上每个元素加上一个层(level)的概念,层高则是随机的, 所以每个元素的高度不一样。每一层都会指向下一个同一层的元素,查询元素时由高层向后向下的方式二级检索从而达到更高的查询效率,下面用图解的方式解析如何读写跳跃表元素的。在看图之前可以先看一下源码,尝试理解一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 跳跃表结构
typedef struct zskiplist {
struct zskiplistNode * header , * tail ; // 记录 head 和 tail 两个节点
unsigned long length ; // 记录长度
int level ; // 记录当前最高 level,如果有新元素插入且其 level 大于当前最高则更新该值
} zskiplist ;
// 跳跃表节点
typedef struct zskiplistNode {
sds ele ; // 元素值
double score ; // score
struct zskiplistNode * backward ; // 向前指向指针,用于往回跳
struct zskiplistLevel {
struct zskiplistNode * forward ; // 每一层都指向下一个同高度元素
unsigned long span ; // 到下一个同高度元素的跨度
} level []; // 该元素的 level 数组,index 从 0 到 N 表示从最低到最高,默认最高支持 32 层
} zskiplistNode ;
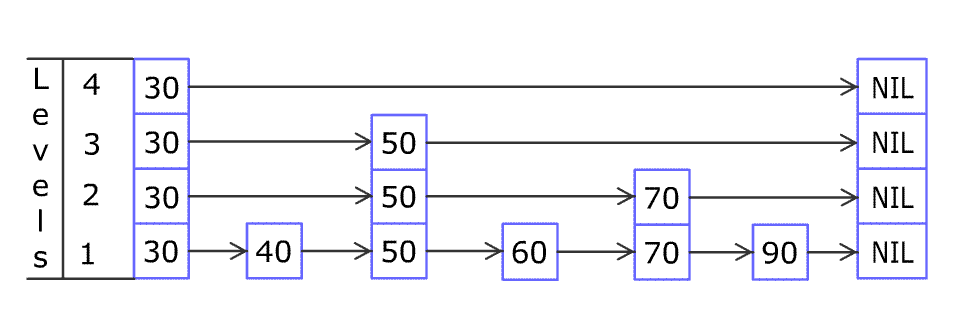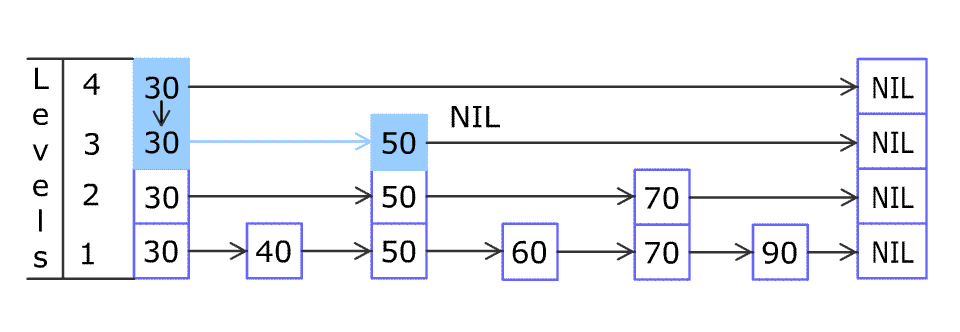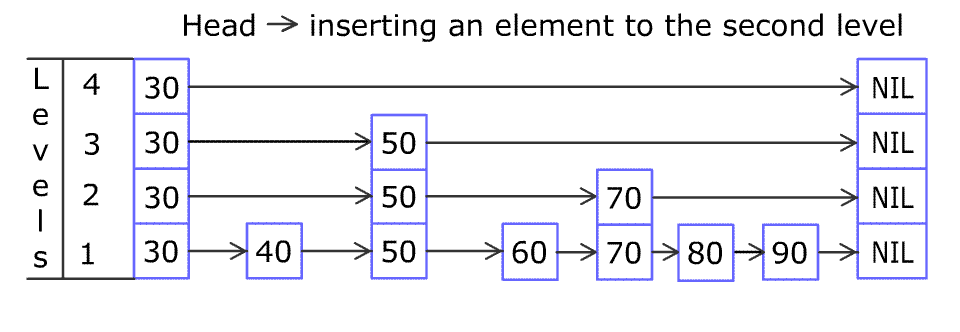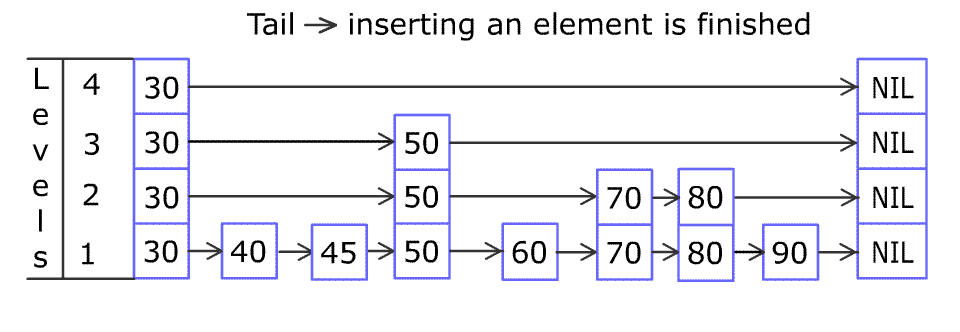
如果看完源码还是没有看到 ,请看下图:
跳跃表结构 从图中可以看到, 跳跃表主要由以下部分构成:
表头(head):负责维护跳跃表的节点指针。 跳跃表节点:保存着元素值,以及多个层。 层:保存着指向其他元素的指针。高层的指针越过的元素数量大于等于低层的指针,为了提高查找的效率,程序总是从高层先开始访问,然后随着元素值范围的缩小,慢慢降低层次。 表尾:全部由 NULL 组成,表示跳跃表的末尾。
图中没有表示出来 zskiplistNode.backward 指针的指向,实际上图中每个元素都会指向前一个元素
3.2.3 查询元素 在跳跃表查询元素,总是从 head 的顶层 level 向后向下的方式取查询,以上面的示例图为例,下面讲解如何查询 score 值为 7 的元素:
初始条件:
p 为初始指针,指向 head 的顶层 level 查询步骤:
判断指针 p 的 forward 元素的值 当满足条件:forward.score < score 或 forward.score == score && forward.ele < targetEle 时,p 向前移动,level 不变
当 p 的 forward 为 null 或者forward 元素的值大于 score 时,level 减一,但是 p 不往前移动
步骤 1,2 一直循环,指到 p 移动到 null 或者移动到目标元素为止。
跳跃表查询元素过程 源码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 下面就是非常常规的一个遍历查找过程 */
x = zsl -> header ;
// 从head 顶层level开始向下遍历
for ( i = zsl -> level - 1 ; i >= 0 ; i -- ) {
// 每一层判断forward元素不为空的时候是否与目标score和ele
while ( x -> level [ i ]. forward &&
( x -> level [ i ]. forward -> score < curscore ||
( x -> level [ i ]. forward -> score == curscore &&
// 这里的 sdccmp 是Redis内实现的对其 String 结构的字符串进行对比(即字典排序的对比)
sdscmp ( x -> level [ i ]. forward -> ele , ele ) < 0 )))
{
x = x -> level [ i ]. forward ;
}
}
然后再真正实现 zset 的时候,不会根据 value 值去遍历查询跳跃表, 而是直接从哈希表查是否存在
3.2.4 添加元素 添加元素核心有以下几点:
找到需要插入的位置,这块用上上一个小节的查询元素相关知识 在查找位置的过程中需要记录牵连到需要更新的元素 如何得到新元素的层高,真的是 [0,32) 之间随机一个数嘛? 如果新元素的层高大于当前 skiplist 的高度,需要做哪些调整工作? 对以上几点有了明确的认知和回答后,了解插入元素的过程就变得很简单。
添加元素过程:
定义一个 zskiplistNode *update[ZSKIPLIST_MAXLEVEL] 数组记录每次变更 level 时的节点(后期更新受影响的节点用)
定义 unsigned int rank[ZSKIPLIST_MAXLEVEL] 数组记录两次向下遍历的节点直接的跨度
与查询元素一样,从 head 的顶层开始向下向前遍历,找到插入的位置,这个位置满足 score 值介于前后的元素
在遍历的过程中,每往下移动一次(level - 1 )的时候记录当前元素update[cur_level] = cur_node
在遍历的过程中,每往前移动一次(注:每次移动只会单向 不会同时向前向下)的前记录同一个 level 内的跨度
rank[cur_level] += cur_node.level[cur_level].span (这里之所以累加是因为,同一个 level 上可能会向前移动 n 次,如上面示例图中的从 1 到 6 的过程都是在同一个 level 上进行的)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 定义变量
zskiplistNode * update [ ZSKIPLIST_MAXLEVEL ], * x ;
unsigned int rank [ ZSKIPLIST_MAXLEVEL ];
int i , level ;
// 从 header 开始遍历
x = zsl -> header ;
// 初始位置 header 的顶层 level
for ( i = zsl -> level - 1 ; i >= 0 ; i -- ) {
/* store rank that is crossed to reach the insert position */
// 如果当前level 为最高一层的 level 则 rank 记录 0
rank [ i ] = i == ( zsl -> level - 1 ) ? 0 : rank [ i + 1 ];
while ( x -> level [ i ]. forward &&
( x -> level [ i ]. forward -> score < score ||
( x -> level [ i ]. forward -> score == score &&
sdscmp ( x -> level [ i ]. forward -> ele , ele ) < 0 )))
{
// 向前移动时记录当前 level 移动的跨度
rank [ i ] += x -> level [ i ]. span ;
x = x -> level [ i ]. forward ;
}
// level - 1 时 记录当前元素
update [ i ] = x ;
}
随机一个 level, Redis 是有一套简单的算法去生成随机的 level 跳转查看 。
如果随机的 level 大于 skiplist 当前最高 level,则在 update 数组记录从当前最高到新的最高之间的level 对应的节点为 head 节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* we assume the element is not already inside, since we allow duplicated
* scores, reinserting the same element should never happen since the
* caller of zslInsert() should test in the hash table if the element is
* already inside or not. */
level = zslRandomLevel ();
if ( level > zsl -> level ) {
// 在 zsl->level 到 level 之间区域补缺原来的空缺
// 原来高于 zsl->level 的 level 均指向 null,现在需要指向到新的元素对应的 level 了
for ( i = zsl -> level ; i < level ; i ++ ) {
rank [ i ] = 0 ; // 因为最高的 level 了所以在该层不会指向下一个元素 所以对应的 rank == 0
update [ i ] = zsl -> header ; // header 需要更新
update [ i ] -> level [ i ]. span = zsl -> length ; // 不再指向 null 所以 span 也需要更新,这里先赋值为最远距离 下面会统一处理
}
// 更新新的 level
zsl -> level = level ;
}
插入新的元素,更新原则的前后指向指针 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 初始化新的节点
x = zslCreateNode ( level , score , ele );
// 从下到上 一层层更新完善前后节点以及相关节点的关系
for ( i = 0 ; i < level ; i ++ ) {
// update 数组一个元素记录的是 每一层最靠近(从header 到 x)x 的元素
// 所以每一层最靠近 x 的元素的 forward 由原来的指向改为 x
// 同样的 x 每一层的 forward 都指向原来每一层的指向的元素
// 好比一个单向链表 a -> c, 插入一个 b 在中间,从 `a.next = c` 变为 `a.next, b.next = b, a.next`
x -> level [ i ]. forward = update [ i ] -> level [ i ]. forward ;
update [ i ] -> level [ i ]. forward = x ;
/* update span covered by update[i] as x is inserted here */
// 这里可能比较绕
// span 为当前位置到下一个元素之间的距离,因为不同 level 的存在,每一层的 span 都不一定相同
// rank[0] 为从 header 到当前新元素置位的总的距离
// x 某一层的 span 为前一个同一层的元素的 span 减去 x 与前一个同一层的距离
x -> level [ i ]. span = update [ i ] -> level [ i ]. span - ( rank [ 0 ] - rank [ i ]);
// 前一个同一层的元素的新的 span = 从header 到新元素的距离减去从 header 到该元素的距离 + 1 (加一是因为新增元素了)
update [ i ] -> level [ i ]. span = ( rank [ 0 ] - rank [ i ]) + 1 ;
}
如果新元素的高度没有比 skiplist 最高 level 高,则在新元素之前的比它更高元素的 level 的跨度加一 1
2
3
4
/* increment span for untouched levels */
for ( i = level ; i < zsl -> level ; i ++ ) {
update [ i ] -> level [ i ]. span ++ ;
}
修改新元素的下一个元素(如果存在下一个元素)的 backward 指针,指向新元素
跳跃表长度+1 完成新增元素
配合动图看源码:
跳跃表插入元素过程 3.2.4.1 随机 level 算法 跳跃表作为一个随机化的数据结构,每一个元素都是有不一样高的 level,查询时通过跳跃 N 个元素的方式提高性能。只要确保不同元素直接的 level 是有一定的差别才能体现出跳跃表的性能,否则很容易退化成链表结构了。
每个 level 的元素数从上到下呈现第 L 层的元素数为 L-1的1/p(其中Redis 中这个 p = 4)。那么SkipList可以看成是一棵平衡的P叉树,从最顶层开始查找某个节点需要的时间是O(logpN)。每个跳跃表节点中的指针数组中的每一层,都指向随后一个指针数组大小大于等于该节点指针数据大小的节点。
那么问题来了,如何确保每次随机时,越高层出现概率越低 越底层出现的概率越高呢?
先给出 Redis 源码:
1
2
3
4
5
6
7
8
9
10
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned. */
int zslRandomLevel ( void ) {
int level = 1 ;
while (( random () & 0xFFFF ) < ( 0.25 * 0xFFFF ))
level += 1 ;
return ( level < 32 ) ? level : 32 ;
}
任意一个数 & 0xFFFF 得到的结果在 [0~0xFFFF] 范围内, 结果小于 0.25 * 0xFFFF 的概率就是 1/4 .
根据概率论可以得出越高的 level 出现(即连续多次出现小于 0.25 * 0xFFFF 才能累加到高 level)的概率越低.
数据如下:
level 概率 1 3/4 2 3/4 * 1/4 3 3/4 * 1/4 * 1/4 4 3/4 * 1/4 * 1/4 * 1/4 … … n $3/4 * (1/4)^{n-1}$
3.2.5 删除元素 删除元素相对新增元素来说简单一些,但是整体思路还是一样的。遍历找到删除的元素,在遍历过程中记录删除后需要更新属性的元素以及 level。
遍历并找到需要删除的位置 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
x = zsl -> header ;
for ( i = zsl -> level - 1 ; i >= 0 ; i -- ) {
while ( x -> level [ i ]. forward &&
( x -> level [ i ]. forward -> score < score ||
( x -> level [ i ]. forward -> score == score &&
sdscmp ( x -> level [ i ]. forward -> ele , ele ) < 0 )))
{
x = x -> level [ i ]. forward ;
}
// 记录每一层需要更新的元素
update [ i ] = x ;
}
/* We may have multiple elements with the same score, what we need
* is to find the element with both the right score and object. */
x = x -> level [ 0 ]. forward ;
// 确定元素 删除
if ( x && score == x -> score && sdscmp ( x -> ele , ele ) == 0 ) {
// 删除方法,需要传入 update 数组 方便 删除完更新涉及到的元素
zslDeleteNode ( zsl , x , update );
}
更新被删元素前的每一层的 span 1
2
3
4
5
6
7
8
9
10
11
for ( i = 0 ; i < zsl -> level ; i ++ ) {
// 如果当前 level 指向 x,则新的 span 是自己当前 span 加上 x 的 span -1
if ( update [ i ] -> level [ i ]. forward == x ) {
update [ i ] -> level [ i ]. span += x -> level [ i ]. span - 1 ;
// 同时修改 forward 指针的指向
update [ i ] -> level [ i ]. forward = x -> level [ i ]. forward ;
} else {
// 如果不指向 x 则 span -1 即可
update [ i ] -> level [ i ]. span -= 1 ;
}
}
修改被删除元素的前的元素的向后指针 1
2
3
4
5
if ( x -> level [ 0 ]. forward ) {
x -> level [ 0 ]. forward -> backward = x -> backward ;
} else {
zsl -> tail = x -> backward ;
}
判断被删除元素是不是最高 level,如果是 level 减到第二高元素高度为止
skiplist 长度减一,删除完成。
3.2.6 更新元素 之所以更新元素放到最后,是因为更新元素没有单独的逻辑,完全依赖上面的知识点。
找到元素
删除元素
插入元素
这就是 Redis 内实现的逻辑,简单易懂。虽然感觉哪里不对,但是好像又没什么毛病。
4 zset 实现 上面关于zset的原理和实现都理解的比较透彻了,如果还有不明白的建议看源码,结合源码上下文更好理解。现在我用 go 语言实现跳跃表。关于压缩表我在这里不会涉及到只实现跳跃表相关代码。
4.1 数据结构定义 数据结构定义基本与 Redis 一致,跳跃表 + map 的组合。其中 map 部分为了提高读写性能,自己实现了一个 map 结构。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// zSet is object contain skip list and map which store key-value pair
type zSet struct {
// smap.Map 为自己实现的原生 map 的封装,之后单独讲一下,之所以自己实现是为了提高性能
m smap . Map // store key and value
// 在元素少于 100 & 每个元素大小小于 64 的时候,Redis 实际上用的是 zipList 这里作为知识点提了一下
// 除非遇到性能问题,否则不准备同时支持 zipList 和 skipList
zsl * zSkipList // skip list
}
type zSkipList struct {
head , tail * zSkipListNode
length int // 总长度
level int // 最大高度
}
type zSkipListNode struct {
value string
score float64
backward * zSkipListNode
levels [] * zSkipListLeve
}
type zSkipListLeve struct {
forward * zSkipListNode
span uint // 当前 level 到下一个节点的跨度
}
4.2 初始化 因为存在一个 header 的虚拟节点,所以初始化的时候需要把跳跃表的 header 以及其每一层都初始化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// new skiplist
func newZSkipList () * zSkipList {
zsl := & zSkipList {
level : 1 ,
// 每一层为空的 ZSkipListMaxLevel 层的 head
head : newZslNode ( ZSkipListMaxLevel , 0 , "" ),
}
return zsl
}
// new node
func newZslNode ( level int , score float64 , value string ) * zSkipListNode {
node := & zSkipListNode {
value : value ,
score : score ,
levels : make ([] * zSkipListLeve , level ),
}
// 初始化每一层
for i := 0 ; i < level ; i ++ {
node . levels [ i ] = & zSkipListLeve {}
}
return node
}
4.3 其他功能 增删改查的代码与上面源码解析的逻辑大致相同,我在这里给出go 语言实现的源码,可以点击查看 。在这里不再讲述这些基础功能的实现,
而是给出一些特殊的方法的实现。
4.3.1 根据排名查找元素 在上面的实现里会看到到处飞的 span 这个属性,但是好像一直没有实际用上,其实在遍历过程中尤其是跟排名相关的操作里这个 span 属性是非常的有用,下面看一下实际用处:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func ( zsl * zSkipList ) findElementByRank ( rank uint ) * zSkipListNode {
var (
x = zsl . head
// 已遍历的距离
traversed uint
)
// 从 head 的顶层开始遍历
for i := zsl . level - 1 ; i >= 0 ; i -- {
// 如果当前level 的下一个元素的距离 + 已经走过的距离 小于 目标排名 -> 向前移动
// 否则 level - 1
for x . levels [ i ]. forward != nil && traversed + x . levels [ i ]. span <= rank {
traversed += x . levels [ i ]. span
x = x . levels [ i ]. forward
}
// level -1 前判断是否达到目标 rank
if traversed == rank {
return x
}
}
return nil
}
因为记录了与下一个元素的距离,根据排名找元素变得很简单高效,只要跳跃对应的距离即可(距离代表的就是跨越多少个元素也就是多少个排名位置)
4.3.2 zrange 实现 zrange 这个命令是使用 zset 时最常用的命令之一, 那底层是怎么实现的呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// start stop 支持负数 负数时表示倒数第几个
func ( zsl * zSkipList ) zRange ( start , stop int , withScores bool ) [] string {
if start < 0 {
start = start + zsl . length
if start < 0 {
start = 0
}
}
if stop < 0 {
stop = stop + zsl . length
}
if start > stop || start >= zsl . length {
return nil
}
if stop >= zsl . length {
stop = zsl . length - 1
}
// 到目前为止是为了处理 start 和 stop 越界问题,并把负数换算成正数 方便下面处理
// 先用上面的方法找到遍历的第一个元素
node := zsl . findElementByRank ( uint ( start ) + 1 )
var (
rangeLen = stop - start + 1
result [] string
)
// 从 start 元素开始遍历
for rangeLen > 0 {
result = append ( result , node . value )
if withScores {
result = append ( result , strconv . FormatFloat ( node . score , 'g' , - 1 , 64 ))
}
// 跳跃表的第 0 层可以看做做是一个链表,这样遍历读取多个元素就很方便了
node = node . levels [ 0 ]. forward
rangeLen --
}
return result
}
如果需要逆向遍历 直接把 node = node.levels[0].forward 改成 node = node.levels[0].backward 即可。
5 总结 写到这里,Redis 如何实现 zset 的原理和源码以及如何用 go 语言自己写一遍都讲完了,下面做个简单的总结。
zset 底层是两种数据结构组成(ziplist, skiplist + dict),根据存储的数据量不同从决定使用哪个 跳跃表是一个树状结构,读写时间复杂度 O(logN) 跳跃表的level 是随机算法算出来的,确保每一层是上一次的 P 倍,level 越低数据分布越密集 如果对 Redis 的源码或者跳跃表比较熟悉的话,go 语言的实现基本没有任何难度,是把理解转换成代码过程 实现过程需要注意的是一些特殊情况,包括边界问题,head 和 tail 的问题以及操作某个元素其牵连到的附近的元素 6 参考链接🔗